In the 1970s British mathematician Sir Roger Penrose discovered sets of shapes that tile the plane non-periodically. One such set is the kite and dart, shown in figure 1.
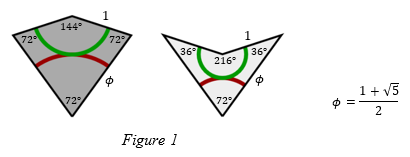
Note the presence of φ, the golden ratio. This number will appear a few more times in these notes.
It is possible for these two shapes to tile the plane periodically, since they can be placed together to form a rhombus, but when placed according to certain rules they form a non-periodic tiling. These rules are indicated by the red and green curves. Tiles can only be placed so that the curves of the same colour in adjacent tiles meet.
Definition 1. A tile that is placed according to the matching rules is said to be legally placed. A tile that is not legally placed is illegally placed.
Figure 2 shows all the ways that tiles can surround a vertex. The names below each tiling were introduced by British mathematician John Conway.
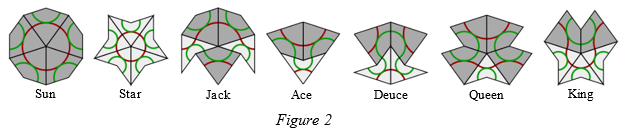
Definition 2. A tiling is said to be legal if its tiles are placed according to the matching rules of figure 1, and the tiling can be continued to cover the infinite plane. A tiling that is not legal is illegal.
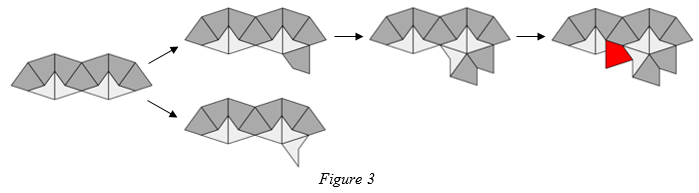
When placing the tiles we sometimes have no choice as to which tile to place next. For example, a dart always forces two kites producing an Ace, shown in figure 2. Sometimes we have a choice as to which tile to place. This can often lead to an illegal tiling. In this case we need to go back and make the other choice. Figure 3 shows that we could place a kite or a dart next. However, if we place a kite and then place the tiles that this kite forces we create an illegal tiling. We have to go back and choose the dart. The curves showing the matching rules have been removed to make it easier to see the tiles.
One way to create a legal tiling covering any sized plane is through a process called inflation. First each tile is decomposed into smaller tiles. A kite is decomposed into two smaller kites and two halves of two smaller darts, and a dart is decomposed into one smaller kite and two halves of two smaller darts. This is shown in figure 4. It is left as an exercise to show that the lengths of the sides of the tiles after decomposition are 1/φ times the lengths of the sides of the tiles before decomposition. The whole tiling is then enlarged by a factor of φ so that each tile is the same size as the tiles before decomposition.
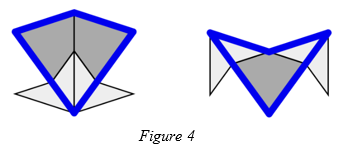
Theorem 1. When we inflate a legal tiling the resulting tiling is also legal.
Proof. If a tiling is legal then each vertex in the tiling will be surrounded one of the tilings from figure 2. Figure 5 shows the decomposition of these tilings.
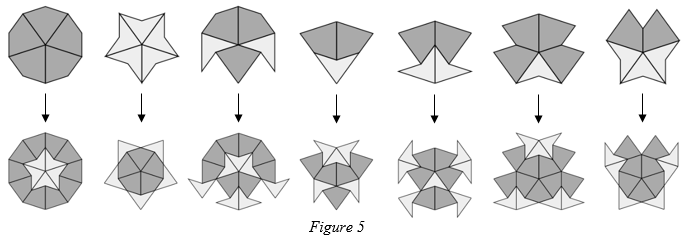
After decomposition no tiling contains any illegally placed tiles. So the decomposition of a legal tiling is also legal, therefore the inflation of a legal tiling must also be legal.
∎
Figure 6 shows the result of repeatedly inflating a tiling.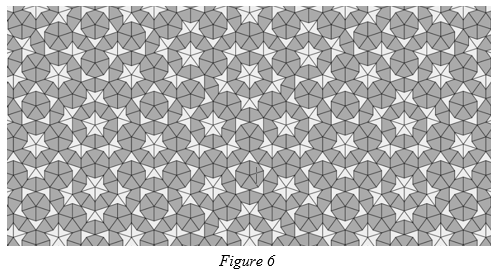
Theorem 2. Every kite and each half of every dart in a tiling are part of a decomposed kite or a decomposed dart.
Proof. Consider the two short sides of a kite. Either both of these sides each touch a dart, creating an decomposed dart, or one of the sides touches a dart and the other a kite, forcing a decomposed kite. This is shown in figure 7.
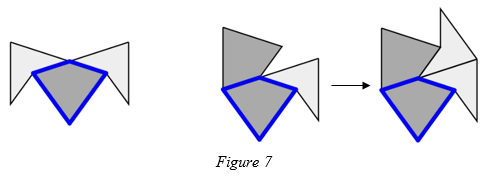
Since a dart always forces two kites at its shortest sides it follows that each half of every dart is part of either an inflated kite or an inflated dart. This is demonstrated in figure 8.
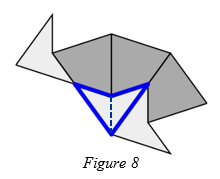This completes the proof. ∎
The reverse process of inflation is called deflation. Groups of tiles are composed to form larger kites and darts (refer back to figure 4). The whole tiling is then resized so that each tile is the same size as the tiles before composition.Theorem 3. All legal tilings can be deflated with the resulting tiling also being legal.
Proof. By Theorem 2 every kite and each half of every dart in every tiling are part of a decomposed kite or a decomposed dart. Therefore it is always possible to deflate a tiling. We need to show that the resulting tiling after deflation is legal.
Let’s consider the tiles which make a decomposed dart. There are two possible ways in which neighbouring tiles can be placed along the longest edge of this decomposed dart. These are shown in figure 9, along with some more tiles that are forced. If we compose each tiling the resulting tiling is legal.
There is only one possible way in which neighbouring tiles can be placed along the shortest edge of a decomposed dart. This is shown in figure 10, along with some more tiles that are forced. If we compose the resulting tiling is legal.
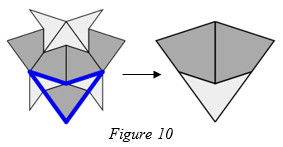
Now let’s consider the tiles which make a decomposed kite. There are two possible ways in which neighbouring tiles can be placed along the longest edge of this decomposed kite. These are shown in figure 11, along with some more tiles that are forced. If we compose each tiling the resulting tiling is legal.
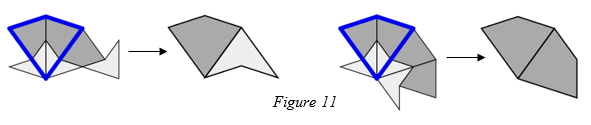
There are two possible ways in which neighbouring tiles can be placed along the shortest edge of a decomposed kite. These are shown in figure 12, along with some more tiles that are forced. If we compose each tiling the resulting tiling is legal.
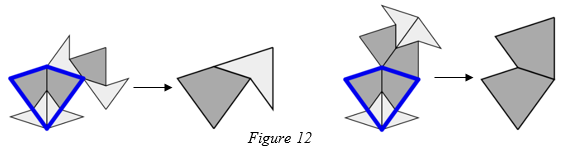
We have therefore shown that any legal tiling can be deflated with the resulting tiling also being legal.
∎
Consider the tiling formed by the repeated inflation of a single kite. After each inflation each kite decomposes into two kites and two halves of a dart (= one dart) and each dart decomposes into one kite and two halves of a dart (= one dart). Figure 13 shows the total number of kites and darts after each inflation.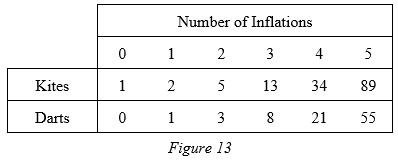
The values in the table appear to follow the Fibonacci sequence. The ratio of two adjacent terms in the Fibonacci sequence coverges to φ, the golden ratio.
Theorem 4. Penrose tilings are non-periodic.
Proof. Consider any tiling covering the plane. We can deflate this tiling as many times as we like. This means that the tiling is the repeated inflation of another tiling. Consider the ratio of the total number of kites to the total number of darts after each inflation. At any stage in the inflation process let k represent the total number of kites and d represent the total number of darts. Since each kite is decomposed into two kites and one dart, and each dart is decomposed into one kite and one dart, as the value of k / d converges we must have
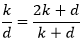Rearranging gives
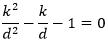Applying the quadratic formula
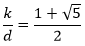
So the ratio of the total number of kites to the total number of darts in a tiling covering the infinite plane is equal to φ, the golden ratio. This is irrational, so the tiling must be non-periodic.
∎
Although Penrose tilings are non-periodic they have some properties that are usually associated with periodic tilings.Theorem 6. Every tile lies within an Ace.
Proof. Every dart lies within an Ace since a dart always forces an Ace. This is shown in figure 14.
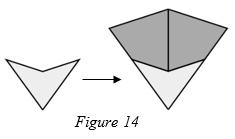
Each kite can touch either two darts at its shortest sides, or one kite and one dart. Both of these arrangements force the kite to lie within an Ace. This is shown in figure 15.
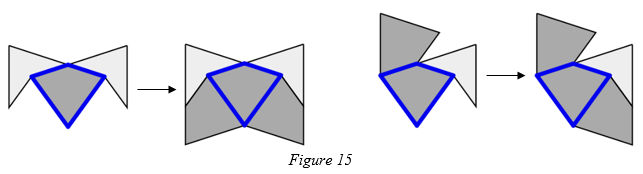This completes the proof.∎
Theorem 7. The seven ways in which tiles can surround a vertex (Sun, Star, Jack, Ace, Deuce, Queen and King) appear infinitely often in any tiling of the plane.Proof. If we deflate a tiling three times then from theorem 6 every tile in this deflated tiling lies within an Ace, so the deflated tiling must contain infinitely many Aces. If we re-inflate the tiling three times to produce our original tiling then each of the Aces are inflated three times. Figure 16 shows a three-times inflated Ace, with some forced tiles added. This must appear infinitely often in the tiling. Since all seven ways in which tiles can surround a vertex are present in the three-times inflated Ace, they must appear infinitely often in the tiling.
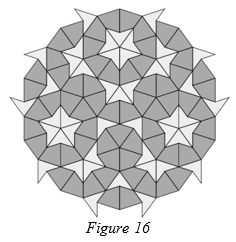This completes the proof.∎
Definition 3. The diameter of a patch of tiles is the diameter of the smallest circle which contains all the tiles in the patch, as shown in figure 17.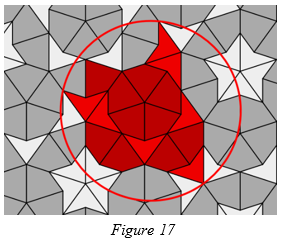
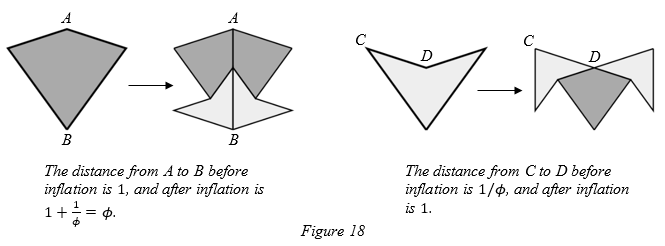
We will write distances and diameters in terms of the length of the longest side of a kite or dart in the tiling. For example, if a patch of tiles has diameter 4 then its actual diamter is 4l, where l represents the length of the longest side of a kite or dart. Notice that when we inflate a patch of tiles then the diameter of the new patch is φ times the diameter of the old patch. This can be seen from inspecting corresponding lengths in single tiles and their inflations. Two examples of such lengths are given in figure 18.
Theorem 8. Any patch of tiles appears infinitely many times in any Penrose tiling.
Proof. When we deflate the tiling the diameter of the deflated patch will be 1 / φ times the diameter before deflation. If we deflate enough times (adding tiles if necessary in order to perform the deflation, but not including the added tiles in the calculation of the diameter) then the diameter of the patch will be less than the length of the shortest side of a kite or dart. This means it will contain a maximum of one of the arrangements from figure 5, the seven ways in which tiles can surround a vertex. By theorem 7 since each of these appears infinitely many times in a tiling, upon re-inflation back to the original tiling the patch of tiles must appear infinitely many times.
∎
Theorem 8 implies that it is impossible to distinguish one Penrose tiling from the next by investigating a finite patch of tiles, since no matter how large a patch of tiles is it will appear infinitely many times in every Penrose tiling. In fact, given a patch of tiles of diameter d there is an upper limit, depending on the value of d, on how far we have to look from this patch in order to find a matching patch of tiles.Consider the seven different ways in which tiles can surround a vertex. In the proof of theorem 7 we showed that each of these arrangements appears in a three-times inflated Ace, and also every tile in a Penrose tiling lies in a three-times inflated Ace. In fact, each of the seven arrangements appears several times times in a three-times inflated Ace.
Figure 19 shows a three-times inflated Ace, with forced tiles added. The blue line indicates the original Ace. The Sun appears within or on the boundary of the original Ace a total of six times.
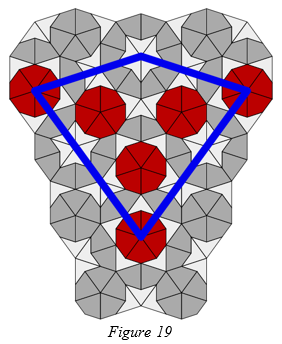
Sun patches which lie outside the boundary of the original Ace in figure 19 must lie within or on the boundary of a different Ace. So by inspecting figure 19 we can deduce that the distance from the vertex of any Sun patch to the vertex of the closest matching Sun patch in any tiling is 2 + 1 / φ.
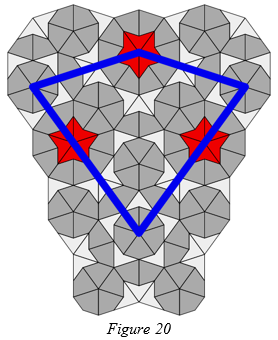
Figure 20 shows the same tiling but with all Stars within or on the boundary of the original Ace highlighted. From this we can deduce that the distance from the vertex of any Star patch to the vertex of the closest matching Star patch in any tiling is 3 + 2 / φ.
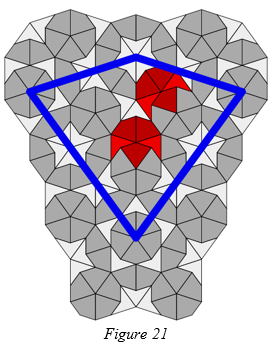
There are many Jack patches within or on the boundary of the original Ace, some of which overlap. If we consider each Jack, one-by-one, and find the closest matching non-overlapping Jack, the pair of Jack patches whose vertices are the furthest apart are shown in figure 21. The distance between them is less than 1 + 2 / φ.
Continuing in the same way we can find the maximum distance we need to look to find a matching patch for each of the seven ways in which tiles can surround a vertex. These distances are shown in figure 22. In some cases the actual distance is slightly less than the value listed.
Theorem 9. Given a patch of tiles of diameter d, a matching patch exists within a distance of 3d.
Proof. If we repeatedly deflate the patch of tiles (adding tiles if necessary, but not including the added tiles when calculating the diameter of the patch) then the diameter will change by a factor of 1 / φ after each deflation. Eventually it will be so small that it will consist of only one of the vertices of a Sun, Star, Jack, Ace, Deuce, Queen or King.
Suppose we are left with a Sun after repeated deflation.
To be continued...
Last updated 30th October 2018.